Basic Concepts on Valuing Earn-Outs – Part III – Discount Rates
Part I and
Part II on
www.withum.com.
On the assumption that we are all on the same page, let’s continue to discount rates. Once the practitioner gets to a place mentally where they understand how to get the risk-adjusted and risk-neutral conclusions to equal, the rest is gravy. The recently released exposure draft from The Appraisal Foundation (TAF), entitled, “First Exposure Draft – Valuation of Contingent Consideration” (Exposure Draft) and publicly available presentations cover these concepts in more detail.
A value conclusion results from combining an estimated benefit stream with the risk of achieving that benefit stream. Valuing a contingent consideration requires incorporating the non-linear benefit stream typically associated with it much as one would consider the non-linear nature of the benefit stream when pricing call and put options. For example, let’s use Daniel Kahn’s (Partner, EY) presentation1 on valuing earn-outs and assume that a 1-year earn-out pays the excess EBITDA above $80. The payoff scheme would look something like this:
Table 1: Sample Payoff on Earn-out
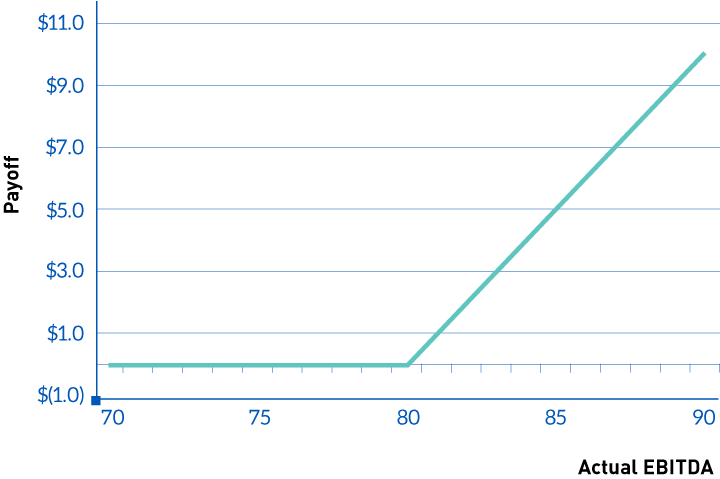
Based on the above table, the non-linear nature of the expected payoff implies that any risk measure has to take into account the kinked pattern and the appraiser has to develop a reasonable payoff date EBITDA estimate. Please note that this payoff is leveraged and based on outside earnings. It should not come as a surprise to anyone that it is risky. The payee is exposed to the same risk that an equity holder faces relative to total equity value of a business.
Discount rates2 capture a combination of default probability and recovery amount. If the payoff is driven by achieving earnings, and earnings are inherently risky, then high discount rates are understandable. Driving this home is the necessary reliance on high earnings to increase the payoff and many zero dollar payoff scenarios coupled with no recovery against this type of liability. But let’s go back to Mr. Kahn’s example to illustrate just how high we are talking about.
In his presentation he asks us to assume that expected EBITDA is $100 and that in all cases it is assumed EBITDA will be above $80 (this would be the case, say, if EBITDA were tied to contracts or other similar types of obligations.) Further, it’s requested that we assume the WACC for this company is 10 percent and the risk-free rate for 1-year is 1 percent.
The payoff amount is then future EBITDA less $80, and so the expected payoff amount is $100 less $80 or $20. We see practitioners in this instance often simply discounting the $20 by 10 percent citing that the uncertainty of the payoff is tied to the performance. This results in a contingent consideration value estimate of $18.18.
As Mr. Kahn points out, this is not correct because the $20 expected payoff consists of two different risk-type cash flows. The $100 is certainly risky at the company’s WACC or 10%. But, the $80 is contractual, and should be discounted at the risk free rate (or 1 percent). This is the leveraged position. Therefore, if you discount each leg of the payoff by its appropriate risk measure, then the resulting value is much lower (i.e. $100/1.1 – $80/1.01 = $11.70).
If the logic around the above calculation makes sense, then the implied discount rate would be $20 / $11.70 or 71%. The leverage position of this example or $80-to-($100/1.1) is 88% percent. The challenge practitioners have is that there is not a directly observable 60, 70, 80 or greater percentage discount rates. One cannot look in the market or formulaically derive (at this time) one with the purpose of entering into a scenario based model. In fact, once you consider payoffs above and below the threshold, caps and floors or a series of possible payoff drivers and terms, using a PWERM (See Part II) in a risk-adjusted framework will not work.
To illustrate how discount rates can increase dramatically due to this leverage concept, the Exposure Draft includes a table of implied discounts based on S&P 500 Call Option prices. Below find an updated table as of March 28, 2017 that compares the market price for an S&P 500 option to a similar option drifted at the S&P’s cost of equity over a period equal to the term of the Option. ^SPX was trading at 2,353 at the time of this analysis and we pulled the option chain expiring March 30, 2018:
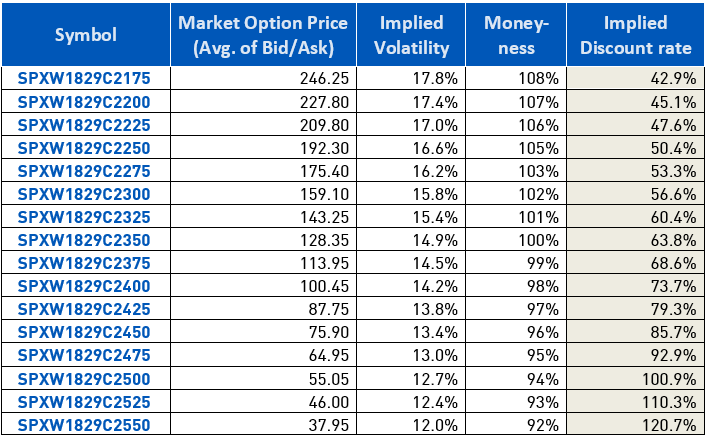
In Part IV, we’ll reconcile a risk-adjusted PWERM valuation to a risk-neutral OPM valuation, and through that exercise solve back for implied discount rates. Suffice to say for the purposes of this article, if the payoff scheme is non-linear, relying on the business risk or counterparty risk alone to discount the payoff will create an erroneous conclusion. Further, unless the non-linear payoff structure mirrors a call or put option, it will be impossible to observe in the market a rate which captures the risk of that benefit stream completely. It will then be up to the audience to determine if the overlap or gap between the risks contemplated in the benefit stream or the discount rate result in an unreasonable contingent consideration valuation estimate.
Ask Our Experts
To ensure compliance with U.S. Treasury rules, unless expressly stated otherwise, any U.S. tax advice contained in this communication is not intended or written to be used, and cannot be used, by the recipient for the purpose of avoiding penalties that may be imposed under the Internal Revenue Code.


